Rotations in Euclidean Space

In this post, we’ll cover rotations in Euclidean Space.

Rotation is a rigid body movement of an object around a central line known as axis of rotation. Rotation can have a sign, a clockwise rotation has a negative magnitude and counterclockwise rotation has a positive magnitude.

Rotations in 2-Dimensions

In 2-dimensions, only a single angle is needed to specify a rotation about the origin, termed as angle of rotation. The rotation is acting to rotate an object counterclockwise through an angle \(\theta\) about the origin.

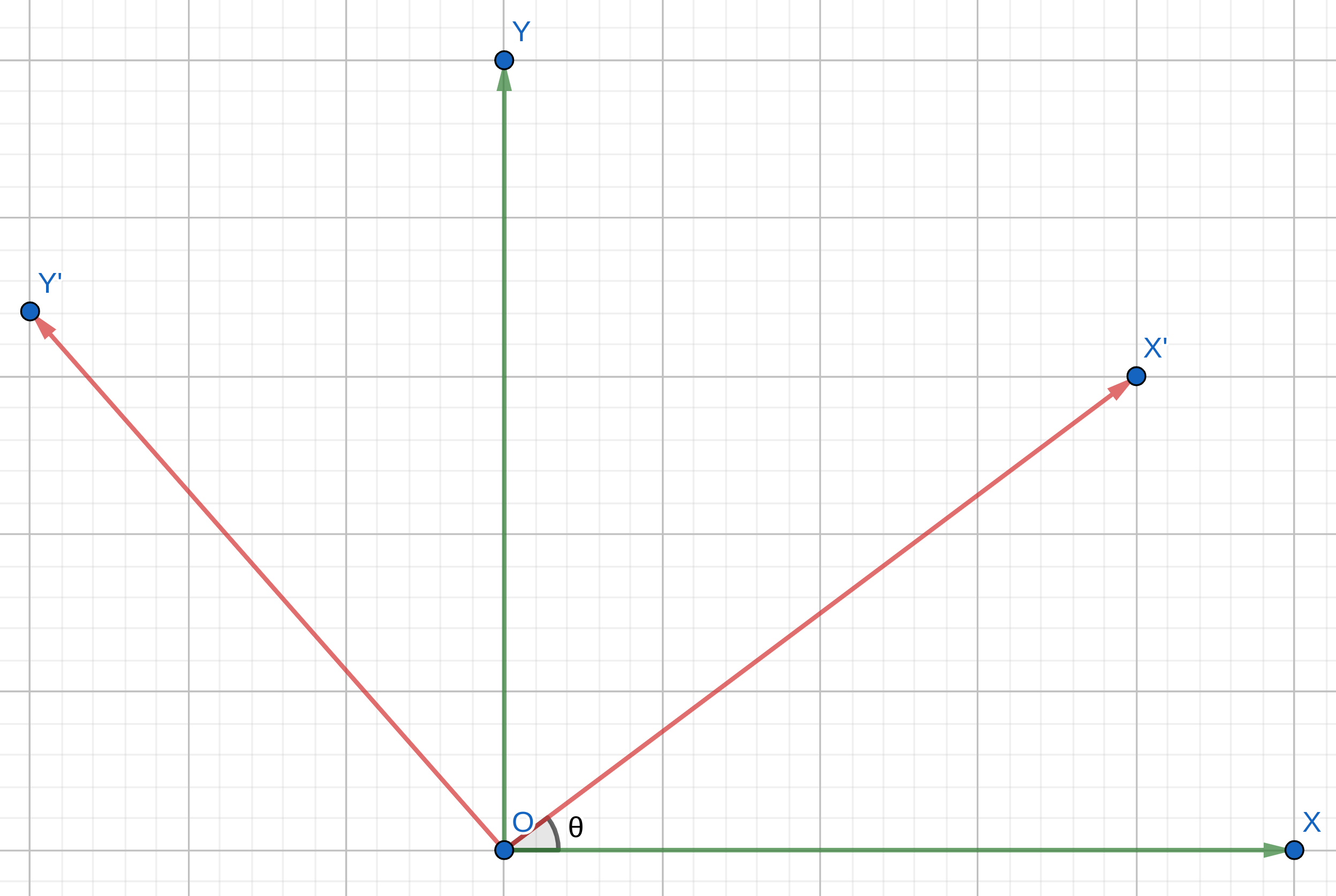
In the above figure, the coordinate frame undergoes a rotation from \(XY\) to \(X'Y'\) by an angle \(\theta\) counterclockwise. Assume the \(Z\) axis as the axis of rotation.

where R is termed as the Rotation Matrix in 2-Dimensions. So any point (in column vector form) in 2-D space can be multiplied with R to get the rotated vector.

The properties of Rotation Matrix:

• Rotation Matrices are Square Matrices
• The determinant of Rotation Matrices is +1, \(det(R) = +1\)
• Rotation Matrices are Orthogonal, i.e \(R.R^{T} = I\).

The proof for the last 2 properties will be provided later in this post.

Rotations in 3-Dimensions

The concept of Rotation matrices can be gently extended to 3-Dimensions. This leads to 3 fundamental Rotation matrices, each along each coordinate axis. The matrices are given below, the reader can verify the same

There are a number of ways in which a general rotation (orientation) can be represented. We will explore 2 such representations in this post

• Axis-Angle
• Euler Angle

Before we start the representations, let’s do some mathematical analysis on these Rotation matrices.

Mathematical Analysis of Rotation Matrices

The set of all orthogonal matrices of size n with determinant +1 is a representation of a group known as the Special Orthogonal Group SO(n), one example of which is the rotation group SO(3).

1. Proof for det(R) = 1 and Orthogonality

   Consider a 3D Rigid Body B. Let’s consider a point \(P_{0}\) denoted by a vector \(v_{0}\) from the origin of the fixed frame. Now, let the body undergo rotation and the new location of the point be \(P_{1}\), denoted by the vector \(v_{1}\).

   \[\begin{equation} v_{1} = R v_{0} \end{equation}\]

   Because the body is rigid, the distance of the point from origin remains same, invariant of any rotation.

   \[\begin{equation} |v_{1}| = |v_{0}| \end{equation}\]

   This implies

   \[\begin{equation} |v_{1}|^{2} = |v_{0}|^{2} => v_{1}^{T}.v_{1} = v_{0}^{T}.v_{0} => v_{0}^{T}.R^{T}.R.v_{0} = v_{0}^{T}.v_{0} \end{equation}\]

   Since this relationship holds for any choice of \(P_{0}\), it must be true that \(R.R^{T} = I\). That is R is an orthogonal matrix. And, we know that \(det(AB) = det(A).det(B)\) and \(det(A^{T}) = det(A)\). Hence,

   \(\begin{equation} det(R.R^{T}) = det(I) = det(R).det(R^{T}) = det^{2}(R) = 1 \end{equation}\).

   Those orthogonal matrices whose determinant is +1 are physically associated with rotations, while those whose determinant is -1 are associated with reflections.

2. Eigenvalues of Rotation Matrix

   Let us denote a general rotation Matrix R as

   \[R = \begin{pmatrix}r_{11} & r_{12} & r_{13}\\\ r_{21} & r_{22} & r_{23} \\\ r_{31} & r_{32} & r_{33} \end{pmatrix}\]

   The characteristic polynomial is given by \(det(R-\lambda I)\)

   \[\begin{equation} det(R-\lambda I) = -\lambda^{3} + \lambda^{2}(r_{11}+r_{22}+r_{33}) - \lambda(cof(r_{11})+cof(r_{22})+cof(r_{33})) + det(R) \end{equation}\]

   where \(cof(r_{ii})\) denotes the cofactor. Now since R belongs to SO(3), det(R) = 1, then \(cof(r_{ii}) = r_{ii}\). This can be shown by considering the columns of R, which are unit vectors and form a right handed orthogonal basis. So

   \(\begin{equation} x = y \times z \end{equation}\) where,

   \[x = \begin{pmatrix}r_{11} & r_{21} & r_{31}\end{pmatrix}^{T}\] \[y = \begin{pmatrix}r_{12} & r_{22} & r_{32}\end{pmatrix}^{T}\] \[y = \begin{pmatrix}r_{13} & r_{23} & r_{33}\end{pmatrix}^{T}\]

   Then,

   \[\begin{pmatrix}r_{11}\\\ r_{21} \\\ r_{31}\end{pmatrix} = \begin{pmatrix}r_{22}r_{33}-r_{23}r_{32}\\\ r_{13}r_{32}-r_{12}r_{33} \\\ r_{12}r_{23}-r_{13}r_{22}\end{pmatrix} = \begin{pmatrix}cof(r_{11})\\\ cof(r_{21}) \\\ cof(r_{31})\end{pmatrix}\]

   Now, the characteristic equation reduces to,

   \[\begin{equation} \boxed{det(R-\lambda I) = -\lambda^{3}+\lambda^{2}(r_{11}+r_{22}+r_{33})-\lambda(r_{11}+r_{22}+r_{33})+1=0} \end{equation}\]

   Letting, \(\begin{equation} \cos \phi = \frac{r_{11}+r_{22}+r_{33}-1}{2} = \frac{tr(R)-1}{2} \end{equation}\) where tr(R) denotes the trace of R. Then,

   \[\begin{equation} \boxed{det(R-\lambda I) = -(\lambda-1)(\lambda^{2}-2 \cos \phi+1) = 0} \end{equation}\]

   Therefore the eigenvalues of R are \(\boxed{\lambda_{1} = 1, \lambda_{2,3} = e^{\pm i \phi}}\)

3. Physical Interpretation of Eigenvalues, Eigenvectors of Rotation Matrix

   Let \(e_{1}\), \(e_{2}\), \(e_{3}\) denote the eigenvectors associated with eigenvalues \(\lambda_{1}\), \(\lambda_{2}\), \(\lambda_{3}\). The eigenproblem is defined as

   \[Re_{j} = \lambda_{j}e_{j}\]

   For the first eigenvalue \(\lambda = 1\), \(Re_{1}=e_{1}\). This physically means, \(e_{1}\) is invariant of R. The set of points in B that lie along \(e_{1}\) remain fixed by rotation. Therefore \(e_{1}\) is the axis of rotation.